반응형
Notice
Recent Posts
Recent Comments
Link
«   2025/05   »
일 월 화 수 목 금 토
1 2 3
4 5 6 7 8 9 10
11 12 13 14 15 16 17
18 19 20 21 22 23 24
25 26 27 28 29 30 31
Tags more
Archives
Today
Total
관리 메뉴

테크매니아

MNIST on FPGA(zynq) : Training and Quantization 본문

카테고리 없음

MNIST on FPGA(zynq) : Training and Quantization

SciomageLAB 2024. 10. 20. 16:36
반응형

개요

이 문서의 목적은 FPGA(zynq-7000)에 MNIST 모델을 올리고 그 내용을 설명하는 것이다.

환경

  • PYNQ-Z2
    • petalinux
  • Windows10 (개발용 VIVADO)
    • VIVADO HLS 2020.1
    • VIVADO 2020.1
  • Ubuntu 18.04.5 (개발용 Ubuntu)
    • Python 3.6.9
  • Google Colab(pro)
    • Python 3.7.10
    • tensorflow 2.5.0
    • Keras 2.5.0

MNIST 모델 학습

우선 포팅 하기 위한 테스트용 모델을 만들어야 한다. 테스트용인 만큼 간단하게 만들기 위해서 Google Colab을 사용해서 jupyter notebook에서 간단히 모델을 만들었다. 복잡한 cnn 모델을 적용하기에 앞서서 Keras 샘플에 있는 것 처럼 Dense 레이어 2개를 이용해서 모델을 만들었다.

모델은 다음과 같이 최대한 간단하게 만든다. use_bias을 False로 줘서 bias없이 weight만 사용 하도록 한다. (이렇게 해도 내가 알기로 아마 크게 성능이 떨어지지 않는다.) 디버깅 과정이 생각보다 복잡해서 최대한 간단하게 만든 모델이다.

사실 cnn 모델도 아니고 FC레이어 3개밖에 안되기 때문에 실제론 배열 곱셈 3개로 숫자를 구분하는 모델이다 보니 적응력(?)이 떨어진다. 학습에 사용되지 않은 이미지로 테스트하면 인식률이 매우 떨어진다. 하지만 성능과 가능성 검토를 위한 샘플이기 때문에 그냥 이렇게 넘어간다.

layer_flatten = keras.layers.Flatten(input_shape=(28, 28))
layer_FC1 = keras.layers.Dense(128, activation='relu', use_bias=False)
layer_FC2 = keras.layers.Dense(64, activation='relu', use_bias=False)
layer_FC3 = keras.layers.Dense(10, activation='softmax', use_bias=False)

model = keras.Sequential([
    layer_flatten,
    layer_FC1,
    layer_FC2,
    layer_FC3,
])
model.summary()
Model: sequential
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
flatten (Flatten)            (None, 784)               0         
_________________________________________________________________
dense (Dense)                (None, 128)               100352    
_________________________________________________________________
dense_1 (Dense)              (None, 64)                8192      
_________________________________________________________________
dense_2 (Dense)              (None, 10)                640       
=================================================================
Total params: 109,184
Trainable params: 109,184
Non-trainable params: 0
_________________________________________________________________

입력 Shape은 (28 * 28)으로 784가 나오고 128, 64 채널의 Dense 레이어 뒤에 10개의 Softmax를 거쳐서 숫자를 구분하게 된다.

원본 full precision 모델이 제대로 학습돼야 한다. 나중에 할 Quantization 단계에서 어차피 오차가 생각보다 크게 발생하기 때문에 최대한 잘 학습해야 한다. 100 epochs이상 돌려서 최대한 학습을 한다.

H5 모델 Export

model.save('mnist_dkdk_FP32_20170708_v1.h5')

학습 후 모델을 h5 파일로 저장한다.

netron으로 h5파일을 열어 보면 학습한 모델이 시각화 돼서 나온다. quantization을 거치지 않았기 때문에 여기 있는 값들은 FP32 값이고, 3개의 Dense 레이어가 있다. 각 레이어 Node를 클릭하면 자세한 정보를 볼 수 있는데, Kernel(weight)값을 확인하고 npy 파일로 내보내기 할 수 있다.

TF나 Keras API를 이영해서 h5 파일에서 바로 가중치 파일을 빼 낼 수도 있겠지만.. 역시 눈으로 값을 확인하기 위해서 3개 Dense 레이어의 값을 모두 직접 내보낸다.

위 이미지와 같이 npy 파일이 내보내 진 것을 알 수 있다. 맨 위에 FC1가 파라미터 개수가 가장 많아서 인지 용량이 크고 점점 작아진다.

이제 이 FP32의 full precision model을 quantization(양자화) 해야 한다. quantization역시 TFLite로 변환 할 때 옵션이 있다. Keras 모델을 TFLite로 Export(?) 할 때 quantization option을 int8로 줘서 quantized model을 Export 할 수 있지만. 이 부분도 직접 했다.

여기서 SQNR(Signal-to-quantization-noise ratio)이라는 개념이 나온다. 신호대 양자화 노이즈 비율 이라는 뜻이라고 한다. 원본 데이터를 quantization 하면 당연히 오차가 생기는데, 이게 얼마나 생기느냐 하는 수치이다. 아마도 TFLite의 quantization을 쓰는게 SQNR이 낮을(오차가 적을) 거지만, 이걸 감수하고 직접 quantization 하는 코드를 작성했다.

Quantization

우선 quantization개념을 이해 해야 한다.

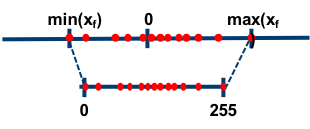위 이미지는 distiller 문서를 참고 했다. 8bit(int8) quantization의 경우, 원본 데이터의 분포를 보고 최소최대값을 0255 값으로 매핑 하는 것이다. 매핑되는 값은 꼭 0255가 아니여도 된다. 10001256과 같이 8bit(256개)로 표현하는 것이 포인트이다. 실제 값은 뭘로 생각해던 무관하다.

실제로 FC1 레이어의 학습된 weight 파일을 보면 값들이 -0.35에서 0.27 사이의 값들이다. (FP32는 표현할 수 있는 범위가 굉장히 큰데 비교적 아주 작은 값만 표현하고 있다.)

┏ -0.3530920147895813                      0.27740925550460815 ┒
├━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┤

┏ -72.0                                                   56.0 ┒
├━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━┤

위 텍스트는 실제 값을 quantization할 때 이해를 돕기 위해 만든 것이다. FC1 레이어의 weight값의 최소는 -0.35, 최대는 0.27이다. 이것을 우리가 표현 할 수 있는 비트 수 8bit (256)개로 표현하기 위해서 256으로 나누면 scale 값이 나온다.

scale = (temp_max - temp_min) / (2 ** (num_bits))

위 수식대로 scale값을 구하면 (0.27 + 0.35) / 256 하면 약 0.002가 나오고 이 값을 모든 FC1 값에 곱하면 양자화 된 값이 나온다.

# Full precision weight FC1
[ -647.91205    -568.53986     334.92346      87.68045      76.24532

# quantized weight FC1
[ -685.21136   -610.45874    291.4603      51.303112    34.92676 ...

위 값은 FC1 레이어의 출력 값이다. (input data와 FC1 weight 값의 행렬 곱셈 결과이다) 값을 보면 오차가 좀 심하게 나긴 하지만 아무튼 전반적인 크기는 비슷비슷하다. (절대값으로 보면 오차가 좀 심하다고 생각할 수 있지만 모델이 간단해서 그런지 추론 결과에 영향을 끼치진 않는다. 신기하다.)

여기까지를 그림으로 정리하면 위와 같다. 맨위는 원본 Full precision model이다. 여기에 quantization을 위한 scale값을 곱하고 정수화 해서 quantized weight를 만드는 것이다.

맨 위 그림의 X는 입력 이미지 라고 했을 때 int8 type이고 W는 Full precision model의 weight이기 때문에 FP32이다. 이걸 quantization하면 세번째 그림의 Wscale은 int8 type이 되고 이렇게 되면 int8 값 간의 행렬 곱셈이 된다. 원본 weight 값에 Scale을 곱했기 때문에 첫번째(원본) Y값과 세번째 Y' 값이 당연히 다르겠지만. Y'을 Scale 값으로 나눠주면 원본 값을 복구(?)할 수 있다.

# Full precision model softmax output
[[1.0000000e+00 0.0000000e+00 3.3974477e-26 0.0000000e+00 0.0000000e+00
0.0000000e+00 0.0000000e+00 0.0000000e+00 0.0000000e+00 1.6024496e-25]]

# # quantized model softmax output
[1.0000000e+00 0.0000000e+00 2.6702990e-20 0.0000000e+00 0.0000000e+00
 6.9595359e-38 8.2144116e-42 3.1713263e-34 8.9683102e-44 1.9113410e-21]

npy파일을 읽어서 FC1 -> ReLU -> FC2 -> ReLU -> FC3 -> Softmax 결과는 위와 같다. 확실히 오차가 매우 크지만 유의미한 특징들은 담고 있는 것 같다.

반응형