테크매니아
Distiller 모델 압축 기법 (1) : Pruning 본문
이 문서는 intel distiller의 docs (https://intellabs.github.io/distiller/pruning.html)를 참고하여 작성하였습니다.
여기서는 Distiller의 모델 압축 기법중 그 첫번째인 pruning에 대해 설명합니다.
Pruning
가중치 및 활성화의 희소성(sparsity)을 유도하는 일반적인 방법론을 가지치기(pruning)라고 합니다. 정리할 가중치를 결정하기 위해 이진 기준을 적용하는 것입니다. 정리 기준과 일치하는 가중치에는 0 값이 할당됩니다. pruning 된 요소는 모델에서 정리 됩니다. 값을 0으로 설정하고 역 전파 프로세스에 참여하지 않도록 합니다.
weights, biases, activations를 제거 할 수 있습니다. biases는 적고 레이어의 출력에 대한 기여도가 상대적으로 크므로 잘라낼 인센티브가 거의 없습니다. ReLU는 음의 활성화를 정확히 0으로 만들기 때문에 일반적으로 ReLU 계층 다음에 희소 활성화가 나타납니다. 가중치의 희소성(sparsity)은 가중치가 매우 작은 경향이 있지만 종종 정확한 0이 아니기 때문에 덜 일반적입니다.
Let's define sparsity
희소성(이하 sparsity)은 텐서 크기에 비해 텐서에서 얼마나 많은 요소가 정확히 0인지를 측정 한 것입니다. 요소의 대부분이 0이면 텐서는 sparsity 한 것으로 간주됩니다. 가장 많은정도는 엄격하게 정의되어 있지 않지만 sparse tensor(희소 텐서)를 보면 알 수 있습니다.
L0 - norm함수는 텐서 x에있는 0 요소의 수를 측정합니다.

즉, 요소는 1 또는 0의 값을 L0에 제공합니다. 정확히 0을 제외한 모든 것은 1의 값에 기여합니다. 매우 멋집니다. (0이 아닌 것의 개수를 알 수 있음). 때로는 밀도, 0이 아닌 요소 (NNZ)의 수 및 sparsity를 거꾸로 생각하는 것이 도움이 됩니다.
밀도 = 1 - 희소성
distiller.sparsity 및 distiller.density를 사용하여 PyTorch 텐서의 sparsity과 밀도를 쿼리 할 수 있습니다.
What is weights pruning?
가중치 pruning 또는 모델 pruning은 네트워크 가중치의 sparsity(텐서에서 값이 0 인 요소의 양)를 높이기 위한 방법입니다. 일반적으로 '파라미터'라는 용어는 모델의 weights와 biases 텐서를 모두 나타냅니다. biases 는 weights 요소에 비해 biases 요소가 거의 없기 때문에 거의 정리되지 않으며 문제의 가치가 없습니다. (weights만 pruning 한다는 뜻인듯)
pruning에는 pruning 할 요소를 선택 하기 위한 기준이 필요합니다. 이를 pruning 기준 이라고 합니다. 가장 일반적인 pruning 기준은 각 요소의 절대 값입니다. 요소의 절대 값은 일부 임계 값과 비교되며 임계값 미만인 경우 요소는 0으로 설정됩니다. (절대값이 작은 값은 대충 0으로 본다는 뜻인듯) 이것은 distiller.MagnitudeParameterPruner 클래스에 의해 구현됩니다. 이 방법의 기본 개념은 L1- 노름 (절대값)이 작은 가중치가 최종 결과 (낮은 돌출성)에 거의 기여하지 않으므로 덜 중요하고 제거 할 수 있다는 것입니다. pruning에 동기를 부여하는 관련 아이디어는 모델이 over-parametrized(초과 매개 변수화) 되고 중복 논리 및 기능을 포함한다는 것입니다. 따라서 이러한 중복성 중 일부는 가중치를 0으로 설정하여 제거 할 수 있습니다.
그리고 pruning을 생각하는 또 다른 방법은 가능한 한 많은 0이 있는 가중치 집합을 검색하는 것으로 표현하는 것입니다. 그래도 밀도가 높은 모델 (pruning되지 않은 모델)에 비해 허용 가능한 추론 정확도가 생성됩니다.
Pruning schedule
정리하는 가장 간단한 방법은 훈련 된 모델을 가져와 한 번 정리하는 것입니다. 일회성 pruning 이라고도 합니다. Song Han, Jeff Pool, John Tran, William J. Dally. Learning both Weights and Connections for Efficient Neural Networks, arXiv:1607.04381v2, 2015.에서 이것이 놀랍도록 효과적이지만 많은 잠재적 sparsity이 미개척 상태임을 보여줍니다. 놀랍게도 그들이 free lunch효과라고 부르는 것입니다. 재교육 없이도 정확도를 잃지 않고 연결을 2 배 줄입니다.
그러나 그들은 또한 pruning 후 재교육 요법을 사용하면 훨씬 더 나은 결과(정확도 손실 없이 더 높은 sparsity)를 얻을 수 있습니다. 이를 반복적 pruning이라고 하며 pruning 이후의 재교육을 종종 fine-tuning(미세 조정) 이라고 합니다. 정리 기준이 반복 사이에 변경되는 방식, 수행하는 반복 횟수 및 빈도, 정리되는 텐서 등을 총칭하여 pruning schedule 이라고 합니다.
반복적 pruning은 어떤 가중치가 중요한지 반복적으로 학습하고 일부 중요도 기준에 따라 가장 덜 중요한 가중치를 제거한 다음 나머지 가중치를 조정하여 가지 치기에서 복구하도록 모델을 재 학습하는 것으로 생각할 수 있습니다. 반복 할 때마다 더 많은 가중치를 제거합니다.
정리를 중지 할 시기의 결정도 일정에 표시되며 pruning 알고리즘에 따라 다릅니다. 예를 들어 특정 sparsity level(희소성 수준)을 달성하려는 경우 가지 치기가 해당 수준에 도달하면 중지합니다. 그리고 필요한 컴퓨팅 예산을 줄이기 위해 가중치 구조를 정리하는 경우 이 계산 감소가 달성되면 pruning을 중지합니다.
Distiller는 정리 일정을 YAML 파일로 표현하는 것을 지원합니다 (그런 다음 PruningScheduler 인스턴스에 의해 실행 됨).
Pruning granularity
개별 가중치 요소 정리를 element-wise pruning(요소 별 가지치기)라고 하며 때로는 fine-grained(세밀한 정리)라고도 합니다.
Coarse-grained pruning(거친 가지 치기)는 structured pruning(구조적 가지 치기), group pruning(그룹 가지 치기) 또는 block pruning(블록 가지 치기)라고도 합니다. 이것은 몇 가지 중요한 요소의 전체 그룹을 pruning합니다. 그룹은 다양한 모양과 크기로 제공되지만 시각화하기 쉬운 그룹 정리는 전체 필터가 제거되는 필터 정리입니다.
Sensitivity analysis
pruning을 통해 sparsity(희소성)을 유도하는 데있어 어려운 부분은 각 레이어의 텐서에 사용할 임계 값 또는 sparsity 수준을 결정하는 것입니다. Sensitivity analysis(민감도 분석)는 pruning에 대한 sensitivity에 따라 텐서의 순위를 매기는 데 도움이 되는 방법입니다.
아이디어는 특정 계층의 pruning 수준 (백분율)을 설정 한 다음 정리를 한 번 수행하고 테스트 데이터 세트에 대한 평가를 실행하고 정확도 점수를 기록하는 것입니다. 매개 변수화 된 모든 계층에 대해 이 작업을 수행하고 각 계층에 대해 여러 sparsity 수준을 검사합니다. 이것은 pruning에 대한 각 층의 sensitivity(민감도)에 대해 가르쳐야 합니다.
평가 된 모델은 특정 가중치 텐서의 *pruning과 관련하여 훈련 된 모델의 성능 동작을 이해하는 것을 목표로 하기 때문에 분석을 실행하기 전에 최대 정확도로 훈련 되어야 합니다.
구조를 *pruning 할 수 있는 것처럼 구조에 대한 sensitivity 분석도 수행 할 수 있습니다. Distiller는 개별 요소의 L1-노름을 사용하여 요소 별 pruning sensitivity 분석을 구현합니다; 그리고 필터의 평균 L1-노름을 사용한 필터 별 pruning sensitivity를 분석합니다.
Hao Li, Asim Kadav, Igor Durdanovic, Hanan Samet, Hans Peter Graf. Pruning Filters for Efficient ConvNets, arXiv:1608.08710v3, 2017의 저자는 sensitivity 분석을 수행하는 방법을 설명합니다.
각 계층의 sensitivity를 이해하기 위해 각 계층을 독립적으로 정리하고 유효성 검사 세트에서 정리 된 네트워크의 정확도를 평가합니다. 그림b는 필터가 제거 될 때 정확도를 유지하는 레이어가 그림 2a의 기울기가 더 큰 레이어에 해당함을 보여줍니다.(??)
반대로 경사가 비교적 평평한 층은 pruning에 더 민감합니다. 우리는 *pruning에 대한 민감도를 기반으로 각 레이어에 대해 *pruning 할 필터의 수를 경험적으로 결정합니다. VGG-16 또는 ResNet과 같은 딥네트워크의 경우 동일한 단계 (동일한 피처 맵 크기)의 레이어가 pruning*에 유사한 민감도를 갖는 것을 관찰합니다. 계층 별 메타 매개 변수가 도입되는 것을 방지하기 위해 동일한 단계의 모든 계층에 대해 동일한 *pruning 비율을 사용합니다. pruning*하기에 민감한 레이어의 경우 이러한 레이어 중 더 적은 비율을 *pruning 하거나 pruning을 완전히 건너 뜁니다.
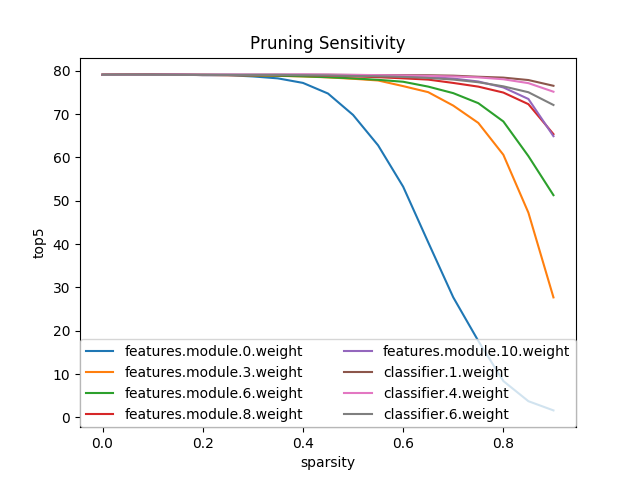
아래 다이어그램은 Distillers의 perform_sensitivity_analysis 유틸리티 함수를 사용하여 Alexnet에서 요소 별 민감도 분석을 실행 한 결과를 보여줍니다.
논문 저자가 보고 하고 다이어그램에 나타난 바와 같이 Alexnet에서 feature detecting 레이어 (컨볼 루션 레이어)는 pruning에 더 민감하며 민감도가 떨어질수록 더 깊습니다. fully-connected 레이어는 대부분의 매개 변수가 있는 곳이기 때문에 훨씬 덜 민감합니다.
 ## References
## References
Song Han, Jeff Pool, John Tran, William J. Dally. Learning both Weights and Connections for Efficient Neural Networks, arXiv:1607.04381v2, 2015.
Hao Li, Asim Kadav, Igor Durdanovic, Hanan Samet, Hans Peter Graf. Pruning Filters for Efficient ConvNets, arXiv:1608.08710v3, 2017.

